TP MeshLab

MeshLab est un très beau logiciel (Open Source) de manipulation et d'édition de maillage 3D à base de triangles (et de quadrilatères). Il fourni un ensemble d'outils pour éditer, nettoyer, corriger, inspecter, afficher, texturer et convertir des maillages...

Il existe sur YouTube de nombreux tutoriels abordant tous les sujets comme ceux de Mister P. (MrPMeshLabTutorials) ou des TUTO thématiques, par exemple : pour l'impression 3D, la texturation à partir de photos, la reconstruction à partir de points scannés (avec EORAD par exemple)...

Normales, rendu et texture mapping sur fichier .obj 

Quelques manipulations sous MeshLab pour vous familiariser avec les maillages de polyèdres et leurs attributs (normales, couleur, texture).

Création d'un tétraèdre coloré aux sommets

Etape 1 : Créez un fichier "tetra.obj" et à l'aide d'un éditeur de texte ascii/neutre (comme Notepad++ par exemple) et ajoutez les lignes nécessaires.
On rappelle que le fichier .obj a un format simple ( voir la doc ), chaque ligne de point commence par un "v" (pour vertex) et chaque ligne de face par un "f" :

v     x   y   z
...
f      n_1 n_2 n_3 ...
...

Chargez ensuite ce fichier tetra.obj sous MeshLab:
  • File/Import Mesh.
Si vous préférez vous pouvez faire l'inverse en générant un tétraèdre sous MeshLab puis en l'exportant au format .obj :
  • Filter/Create New Mesh Layer/Tetrahedron
  • File/Export Mesh

Etape 2 : Associez les couleurs Rouge Vert et Bleu aux sommets (le dernier restera gris) soit à l'aide de MeshLab (Menu Z-Painting (symbolisé par un pinceau), . Faites une copie d'écran et sauvez le fichier. Où sont stockées les couleurs ?

Si vous préférez vous pouvez faire l'inverse en affectant les couleurs aux sommets directement dans le fichier "tetra.obj" à l'aide de l'éditeur de texte.

Vous trouverez ici plus d'information sur le format du fichier OBJ.
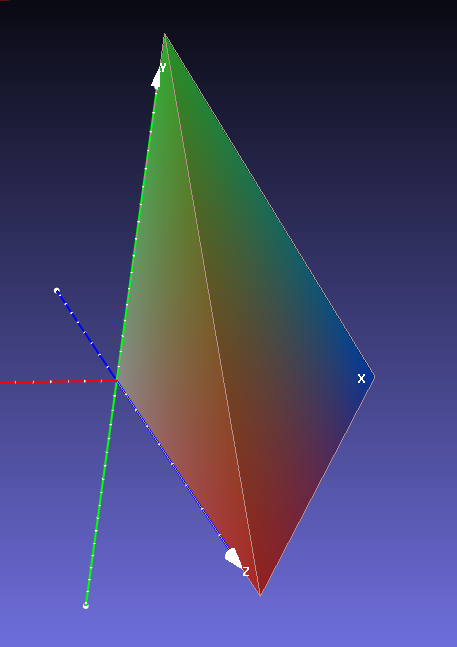colored tetra


 Le dodécaèdre : polyèdre régulier à 12 faces pentagonales
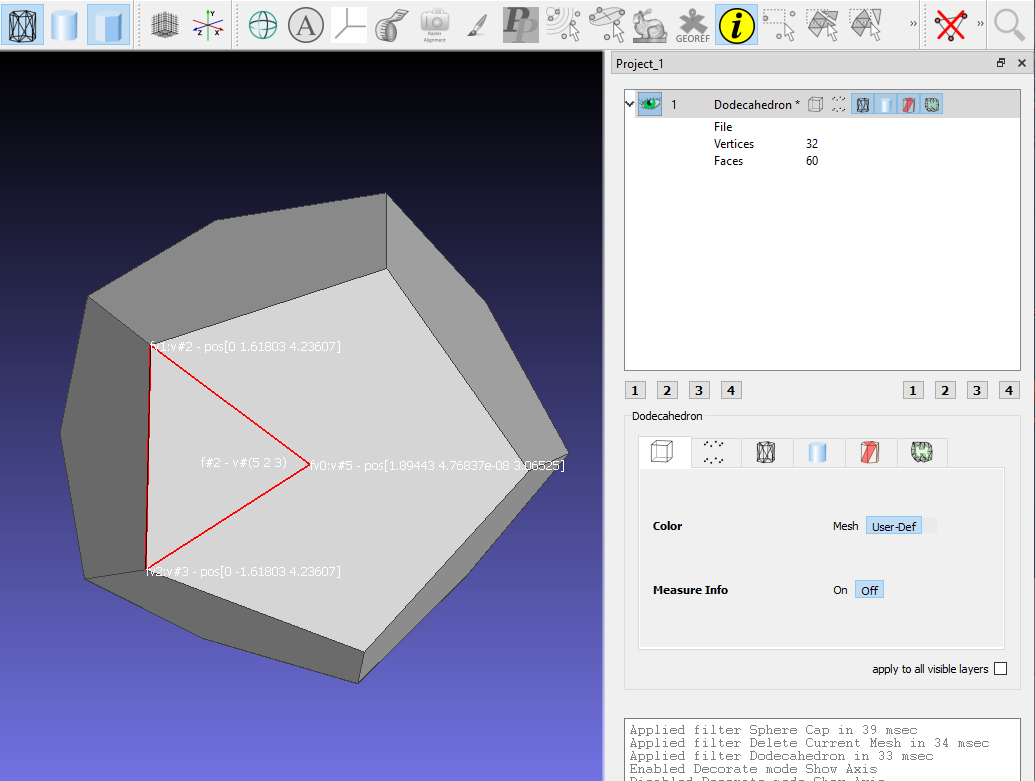
Générez un dodécaèdre avec MeshLab :
Filter/Create New Mesh Layer/Dodecahedron

Verifiez la relation d'Euler : f-a+s=2

Affichez les faces : menu (i)
Que remarquez-vous ?


Exportez en format .obj
Editez le fichier (avec Notpad++ ou équivalent) et décrivez le résultat. Comparez le nombre de faces dans MeshLab à celui du fichier. Qu'en déduisez-vous ?

Rechargez le fichier et analysez le résultat sous MeshLab. Concluez.
 dodecaedre



Definition des matériaux pour le rendu
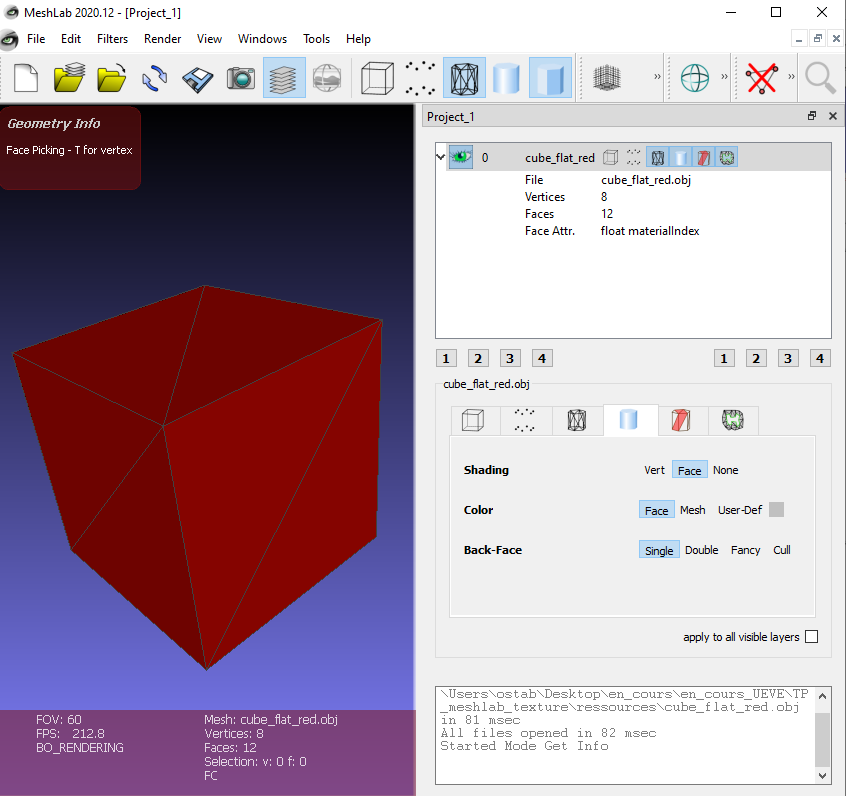
Chargez le fichier "cube_flat_red.obj" dans MeshLab :
  • File/Import Mesh
Verifiez la relation d'Euler : f-a+s=2

Editez le fichier avec un éditeur (NotePad++ par exemple) et expliquez le format : que signifie "vn"
que sépare les slashs dans la description des faces  "f  a//c ..." 


Où se trouve la définition des couleurs ?
Passez le cube en bleu


 red cube

Un cube avec mapping de texture
Téléchargez les ressources nécessaires ici. Dézippez puis ouvrez le fichier "cube_flat_textured.obj" dans MeshLab
  • File/Import Mesh
Editez le fichier avec un éditeur (NotePad++ par exemple) et expliquez le format : que signifie "vt"
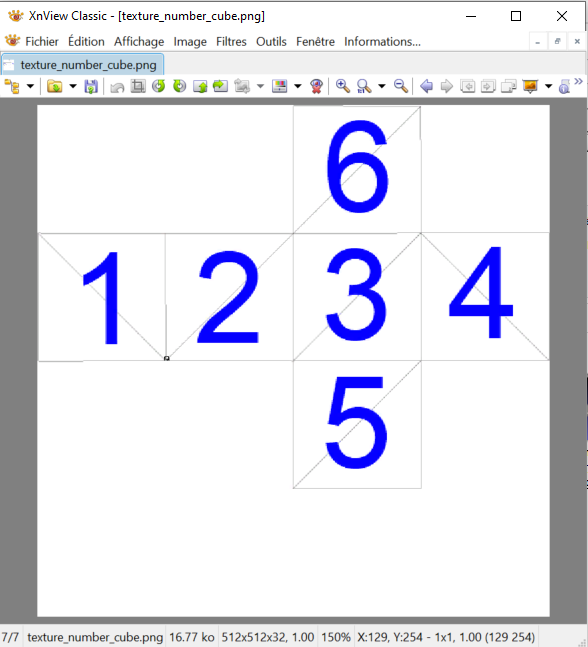
que sépare les slashs dans la description des faces  "f  a/b/c ..." 

L'image de texture à mapper est donnée par :
  • usemtl texture_number_cube.png

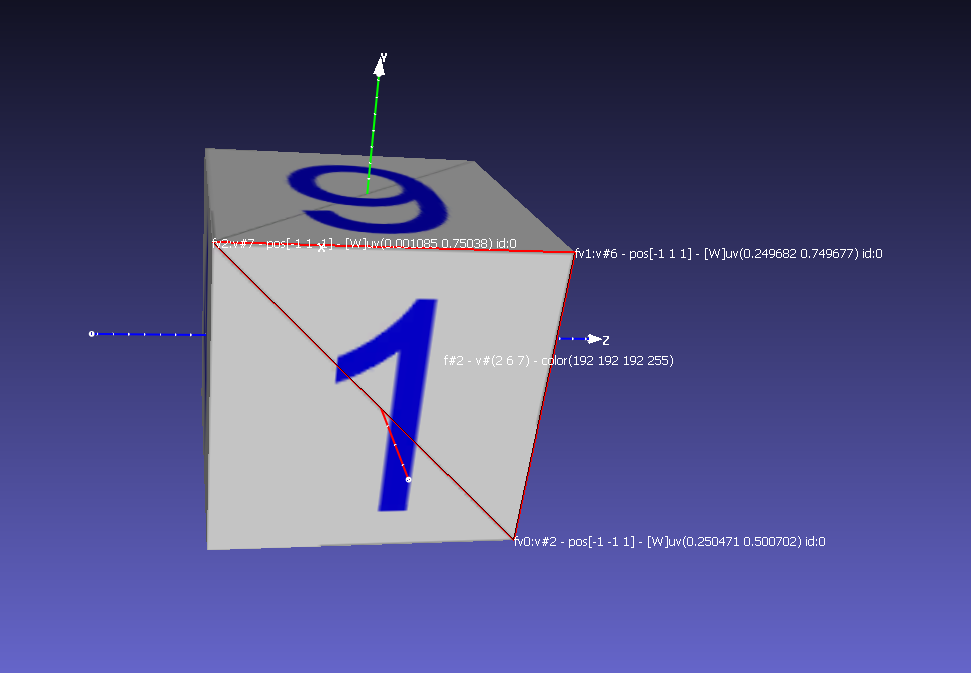
Vérifiez que la face numéro 2 dans MeshLab a une normale orientée  suivant l'axe -x.

Reperez les sommets correspondants ainsi que les coordonnées des textures (u,v)

Retrouvez la face correspondnate dans le fichier .obj. Vérifiez les coordonnée des points, les normale aux sommets et concluez que la face est plate.

Que pouvez-vous dire sur les numérotations dans MeshLab et dans le fichier .obj ?

texture mapping on cube
Chargez l'image correspondant aux textures :
  •  texture_number_cube.png
Avec un programme adhoc (xnview par exemple): affichez les coordonnées des pixel (ici en bas sur le bandeau de l'image à droite).

Donnez les coordonnées dans l'image (i,j) correspondant aux sommets du triangle n°3 dans le fichier .obj. Comment sont orientés les axes dans l'image ?


Donnez la fonction de mapping qui permet de passer des coordonnées locales normalisées (u,v) aux pixels de l'image .png :


i(u) =
j(v) =

Vérifiez numériquement le résultat sur la face n°2 (dans MeshLab).

texture image coordinates