|
This tutorial
gives a gentle introduction to Hidden Markov Models as mathematical abstractions
and relates them to their use in gesture recognition. More precisely, the goal
of this tutorial is to familiarise the audience with HMMs and the way they can
model and recognize gestural procedures. Moreover, it provides the possibility
to learn how to configure the internal states of an HMM as well as its topology
in a way that the model fits better with real-life situations.
Démarrage
Download and unzip the
files TP_HMM-Offline.zip, HMM_RealTime.zip and TP_DTW_offline.zip.
Introduction
Hidden Markov Models (HMMs) are
stochastic models that are commonly used to model and recognize human gestures.
Each of these states corresponds to a pair of probabilities: a) the probability
of transition from one state to another and b) the probability of having
specific values of observations. In case of expert technical gestures, each
effective gesture of the craftsman or the worker can be associated to a HMM,
while the elementary phases of each gesture constitute internal states of the
HMM. According to the modelling proposed, these gestures define the gesture
dictionary GD={G1, G2,… Gn}.
According to the HMM theory, the
gestures have to be modelled before the machine learning procedure, where the sequences
of features (otherwise sequence of observation vectors) are used to
train the models.
Let S={S1, S2,…
SN} be a finite space of states, corresponding to all the
elementary phases of a gesture. A hidden sequence of states Q={q1, q2,…}
is also considered. The transition probability aij=P(qt+1=Sj
| qt=Si) between the states i and j
is given in the transition matrix A={aij}. A given sequence
of hidden states Q is supposed to generate an obvious sequence of observation
vectors Β={o1, o2,…}. We assume that the vectors ot
depends only on the state qt. From now on, the likelihood that the
observation q is the result of the state o will be defined as P(Βt=ot | qt=Si). It is important to outline that
according to the theory of HMMs, each internal state of the model depends only
on its previous state. Consequently, the set of the models for all gestures is GM={λ1, λ2,… λn} where λ=(A, B, π) are the parameters of the model, where
πi=P(q1=Si) is the initial state
probability.
Experiment 1
In this experiment
we will get familiar with the notions of Confusion Matrix, Precision and
Recall, which are very important for the evaluation of any gesture recognition
system. Some questions will be asked to you. Please answer them one by one by
putting your name as the name of the text file.
To do so, please
enter in the folder HMM_Offline and run the TP_HMM.exe.
Then, you should
indicate the file that contains the gestural data by typing the name
TP_HMM.grt. Then it will be asked to you to type a number for the clusters to
be used by the K-Means algorithm, the topology of the HMM and the number of the
internal states for all the HMMs. Please ask for 4 clusters, a left-to-right
HMMs with 7 internal states.
Normally you
should get a similar screen:
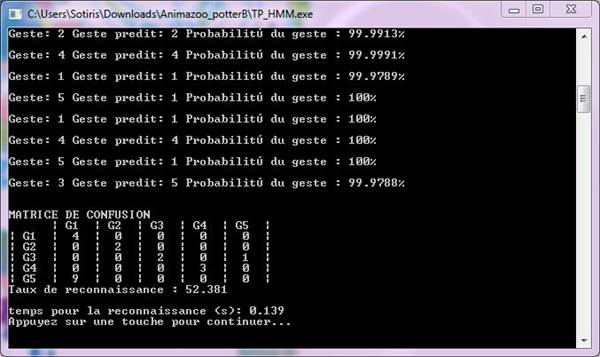
As you see there
are lists of gestures in both the first line and row. Those in the line
correspond to the HMM models that have been trained and those in the row
correspond to the input gestures that have been given for recognition.
1/ How can you
interpret the content of the confusion matrix?
Please repeat
exactly the same procedure 4 more times and copy-paste the values into file
sheet.
2/ Can the values
of the confusion matrix change from one iteration to the other? If yes, why?
Please add the
values for each gesture of all the 5 confusion matrices in order to compute a
total confusion matrix. Then, calculate the Precision and Recall of the system
following the formulas below:
![]()
and
![]()
3/ What is the
difference between "Precision and Recall", and, the "Recognition
Accuracy" provided below each confusion matrix?
4/ Which HMM has
the lowest performance and which the highest?
Please exit from
the TP_HMM.exe
Experiment 2
Within the folder
HMM_Offline you will find 3 sets of data from pottery gestures. More precisely,
it is provided to you the file Animazoo_potterA.grt (data extracted from the
gestures of a Greek potter, by using inertial sensors) and the files
Animazoo_potterB.grt and Kinect_potterB.grt (data extracted from the gestures
of a French potter, by using synchroniously Kinect and Animazoo).
It has been asked
to the potter A to create 5 bowls of 18-20 cm of diameter, 10 cm of height and
approximately 1,3 kg of clay. Additionally, it has been asked to the potter B
to create bigger bowls of the same shape with the potter A, with 20-23 cm of
diameter and 13 cm of height with 1,75 kg of clay. All gestures have duration
of 15-25 seconds and they can be segmented into 4 phases.
The first phase
in the centring and bottom opening, consists on fixing of the clay on
the wheel, hands are pressing with stability on the material aiming at the
opening of the bottom.
Then, the hands
of the potter are picking up the clay, defining the height of the bowl through
the second gesture, the raise of the clay.
Then the body
posture is changing, slightly turning on the right or on the left side for the
first configuration of the shape, for the third phase. Precise finger
gestures are specifying the basic form of the object. The fingers of the one
hand are fixing the clay and of the other are forming the object. His hands are
too close to each other, touching the inner and outer sides of the clay
respectively.
After this stage, the potter is making the final configuration of
the shape. His fingers are controlling and equalizing the bowl thickness and at
the end the potter passes a very fine wire between the bowl and the wheel in
order to take the bowl.
|
|
|
|
|
|
|
4
basic gestural phases |
G1 Centering and bottom opening |
G2 The raise |
G3 The first configuration |
G4 The final configuration and removing |
Now that you have
your first experience in pottery, open in the notepad the files
Animazoo_potterB.grt and Kinect_potterB.grt (numbers above the line
"TimesSeriesData").
1/ What kind of conclusions
can you extract when looking at the data of the different sensors? Is there any
difference?
Please close
these files and run the TP_HMM.exe. Give as file name the Animazoo_PotterB.grt.
Introduce 4 clusters, define an ergodic model with 4 internal states.
If you edit the
file HMMModel.grt you should receive transitions matrices similar as:
|
A1 |
A2 |
||||||
|
0.93 |
0.01 |
0.00 |
0.06 |
0.96 |
0.01 |
0.00 |
0.03 |
|
0.00 |
0.46 |
0.54 |
0.00 |
0.00 |
0.99 |
0.01 |
0.00 |
|
0.00 |
0.45 |
0.55 |
0.00 |
0.00 |
0.00 |
0.99 |
0.01 |
|
0.00 |
0.00 |
0.00 |
1 |
0.00 |
0.00 |
0.00 |
1 |
|
A3 |
A4 |
||||||
|
0.25 |
0.25 |
0.25 |
0.25 |
0.97 |
0.01 |
0.01 |
0.01 |
|
0.25 |
0.24 |
0.25 |
0.26 |
0.00 |
0.99 |
0.01 |
0.00 |
|
0.24 |
0.25 |
0.25 |
0.26 |
0.00 |
0.00 |
0.84 |
0.16 |
|
0.26 |
0.25 |
0.24 |
0.25 |
0.00 |
0.00 |
0.72 |
0.28 |
2/ How can you
verify that the transition matrices are valid?
3/ How do you
perceive the effect of the different transition matrices on the sequences obtained
during the current experiment?
When observing
the A2, we could conclude that HMM2 rules the order in which the states are
browsed because we can easily observe high probabilities on staying at the same
state. Moreover, A3 allows more for frequent jumps from one state to any other
state. Looking back to the pottery gestures, this effect can be explained by
the fact that the G3 is the most complex of all the gestures since the potter
performs sequential micro-movements to fix the clay and adjust the form of the
object. Finally, A4 specifies high probabilities of staying in a particular
state and this can be justified by the small number of internal phases of the
gesture together with
Please do exactly
the same experiment with the same data by using left-to-right HMMs.
4/ Are there any
differences between the ergodic and left-to-right HMMs? Is the use of 4
internal states for all the models an appropriate solution?
Experiment 3
In this
experiment, we will work on a human-robot collaborative use case. An operator
has to work with a robot; we want the robot to recognize the operator gesture’s
to be synchronized with him. We chose 5 gestures.
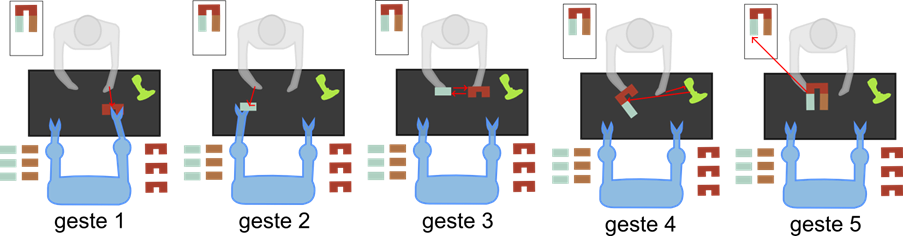
Gesture 1: to take a piece
in the left claw
Gesture 2: to take a piece
in the right claw
Gesture 3: to assemble two
pieces together
Gesture 4: to screw
Gesture 5: to put the
final piece in a box
We recorded the movements of the two hands of several operators using a
Kinect and a tacking algorithm. The gestures were grouped in databases called
“operator1.grt” and “operator2.grt”.
You can choose
whether to use a left-to-right or an ergodic topology for you models. Then,
please do an appropriate number of tests by modifying the parameters of your
models in order to determine those that give the highest Precision Recall for
two datasets. Please also note that the Precision and Recall should be based on
the results of the Confusion Matrices for at least 5 iterations. Finally, you
are kindly asked to plot your results by using Excel.
1/ Which kind of
model fits better with the gestures of the operator A? Is it the same for the
operator B?
2/ Did you find
any difference on the modelling by using the different datasets of the Potter
B?
3/ Which modelling
would you propose for the modelling of operators gestures?
4/ Open the file
“TP_DTW_offline”. Run the executable “TP_DTW” with the same datasets. Do you
have the same results? Why ?
Experiment 4
In this experiment, we will try the real-time gesture recognition. As you know, the mouse can be considered as a 2D motion capture sensor. To do so, you are kindly asked to enter in the folder HMM_Real_Time and run the ConsoleApplication1.exe. Then, a console and the window "Test reco" will open. When the window "Test reco" is selected, you can press "l" to change the dataset or "t" for training the models. The training of the models can take several seconds. When finished, you will receive a message "Model Trained: Yes" in green as well as an histogram with 4 columns that correspond to the likelihood of each gesture.
Here are the 4 gestures to do in real-time with the mouse: a) go left, b) go down, c) go right and d) go up. Enjoy it.
1/ What happens if you perform the gestures the other way around?
2/ What happens if you perform the gestures in an isolated way?
Finally, you are kindly
asked to train the system with your own gestures and test it in real-time.