T.P. "ALGORITHMES GENETIQUES"

Fabien Moutarde, centre de Robotique (CAOR)

Principe du TP

Le but de ce TP est d'abord d'illustrer le fonctionnement des algorithmes génétiques sur deux exemples, et de souligner l'importance de quelques uns des principaux paramètres de ces algorithmes (codage, taille de la population, probabilité de mutation, fonction d'évaluation).
Enfin, un troisième exercice est proposé sur un problème plus sophistiqué : produire un comportement "intelligent" d'un robot virtuel dans un environnement aléatoire.

Préalables

Pour ce TP, bootez de préférence sous Linux (en théorie, tout peut s'effectuer indifféremment sous Linux ou Windows, mais l'exercice 3 nécessitant de lancer java depuis un terminal, Linux sera probablement plus commode que Windows...).

Créez dans votre "homedir" (sous /export/home/manitou/....) un répertoire pour ce TP, nommé par exemple TP-genAlgo ("mkdir TP-genAlgo"), puis placez-vous dedans ("cd TP-genAlgo") ;
Téléchargez le fichier tp-algoGen.zip dans votre répertoire TP-genAlgo situé sous votre homedir ;
Décompressez le fichier en question ("unzip tp-algoGen.zip") : vous devriez obtenir (dans le répertoire où vous avez décompressé) 4 fichiers jar "auto-exécutables", et plusieurs fichiers de données.

Exercice 1 : recherche du maximum d'une fonction à une variable

Pour démarrer, exécutez le fichier demo-GA-maxFonc.jar (double-cliquez dessus, ou bien faire java -jar demo-GA-maxFonc.jar dans un "terminal").
NOTE : si le double-clic sur le fichier jar ne fonctionne pas, il suffit, dans l'explorateur de fichier, de faire clic-droit à la souris sur un fichier .jar, d'aller dans l'onglet "Ouvrir avec", puis d'appuyer sur le bouton "Ajouter", et enfin de mettre à l'endroit prévu la commande "java -jar %s" (ceci définira pour la suite l'action que l'ordinateur effectuera quand on double-clique sur un fichier de type .jar).

Dans ce problème, une fonction présentant plusieurs maxima locaux (ce qui rend inapplicables les algorithmes les plus simples de recherche de maximum) est définie sur un certain intervalle et le but est de déterminer à l'aide des algorithmes génétiques l'abscisse du maximum global (sur l'intervalle) de la fonction. On va donc utiliser une population dans laquelle chaque individu correspond à une abscisse située dans l'intervalle (et sera représenté par un trait vertical allant du bas de la fenêtre jusqu'à la valeur de la fonction en ce point).

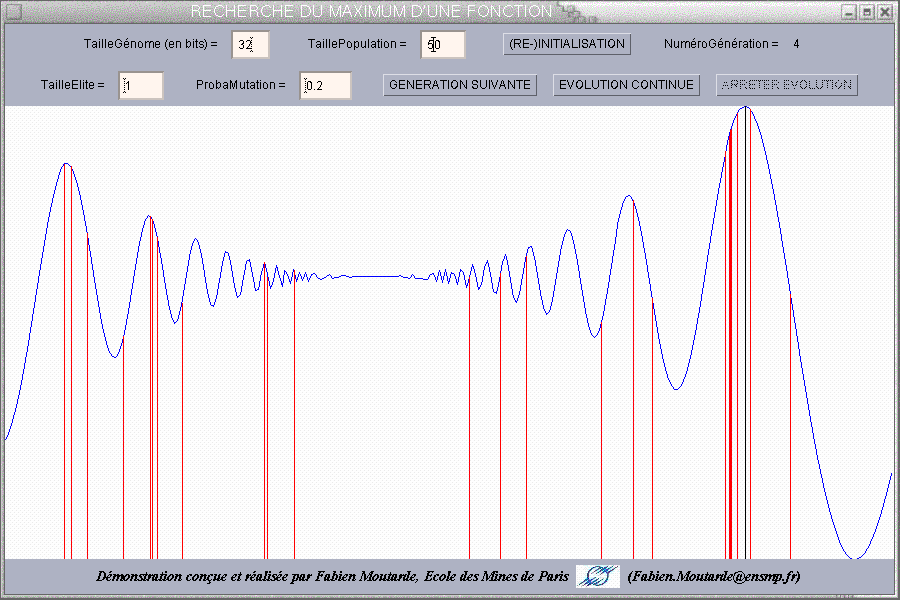
Une des premières questions qui se posent est celle du codage : à quelle séquence de gènes faire correspondre une abscisse de l'intervalle ? On a fait le choix de prendre chaque gène égal à un bit, et de faire correspondre à chaque génome (du type 10011100...) l'abscisse x = xMin + N*(xMax-xMin)/Nmax où N est l'entier dont la représentation binaire est donnée par le génome, et Nmax est le plus grand entier repésentable avec le nombre de bits correspondant à taille du génome. Il ne reste donc plus qu'à choisir le nombre de bits constituant le génome de chaque individu.
Testez diverses valeurs pour cette taille de génome et générez pour chacune plusieurs populations initiales aléatoires en cliquant sur le bouton "(RE-)INITIALISATION", et constatez qu'il faut qu'elle soit suffisamment grande (typiquement >=10) pour qu'assez de valeurs d'abscisse soient atteignables.
Testez ensuite l'impact du nombre d'individus de la population : si celui-ci est trop petit, il faut beaucoup plus de générations pour atteindre le maximum, car il n'y a pas assez de variété dans la population initiale, et seules les mutations finissent par permettre à l'algorithme de converger.
Testez enfin l'influence de la probabilité de mutation : si elle est trop faible, l'algorithme est susceptible de se bloquer dans un maximum local au lieu de converger vers le maximum global.

Remarque : cette démonstration a un but uniquement pédagogique et illustratif, puisque vous constaterez que le nombre total d'abscisses testées avant d'atteindre le maximum global (égal au nombre de générations multiplié par la taille de la population) est généralement tel qu'on aurait un aussi bon résultat en répartissant simplement ce nombre d'abscisses uniformément sur l'intervalle puis en cherchant Max(f(Xi)). L'intérêt des algorithmes génétiques pour la recherche de maximum de fonction n'est en pratique réel que dans le cas d'une fonction à beaucoup de variables, car alors toute exploration systématique de l'espace des n-uplets possibles devient prohibitive, tandis qu'un algorithme génétique peut rester efficace. Malheureusement, la visualisation de la recherche du maximum d'une fonction à n variables est problématique pour n=2, et devient carrément impossible (ou en tout cas incompréhensible) pour n>=3...

Exercice 2 : recherche de la sortie d'un labyrinthe

Pour démarrer, exécutez le fichier demo-GA-labyrExit.jar (double-cliquez dessus, ou bien faire java -jar demo-GA-labyrExit.jar dans un "terminal").

Dans ce problème, un "robot" se déplace dans un labyrinthe, et s'arrête dès qu'il se cogne contre un mur, revient sur un emplacement qu'il a déjà visité, ou a atteint la sortie. Le but est de trouver un parcours menant à la sortie (marquée par une croix verte). On va donc utiliser une population dans laquelle chaque individu correspond à un ensemble de décisions de direction à prendre (et sera représenté uniquement par sa trajectoire dans le labyrinthe).

De nombreux types de codages très différents sont envisageables, depuis une succession d'ordres "Droite-Droite-Bas-Gauche-..." jusqu'à la représentation d'une fonction de décision dépendant de ce que le robot "voit" dans son environnement immédiat et de l'historique complet de ses actions et perceptions antérieures. On a ici choisi de ne pas tenter de faire des robots "intelligents", mais de se limiter à des robots en quelque sorte "pré-programmés", avec un codage indiquant au robot quelle direction il doit prendre en fonction de son seul emplacement : comme il y a pour chaque case 4 orientations possibles dans l'absolu (indépendamment des murs) et N cases constituant le labyrinthe, on a adopté comme génome pour chaque individu une séquence de 2*N bits (2 bits par case).
Comme dans l'exemple précédent, la taille de la population et la probabilité de mutation ont une influence sur l'efficacité de l'algorithme génétique, mais l'intérêt essentiel de ce deuxième exemple est de mettre en évidence l'importance et la difficulté du choix de la fonction d'évaluation des individus :

une approche simpliste ("ExitFound") consiste à donner une "note" ne dépendant que du fait que le robot ait atteint ou non la sortie ; l'ennui est qu'alors tous les robots ne trouvant PAS la sortie ont la même note, ce qui fait que l'algorithme génétique se résume alors à une recherche totalement au hasard : pour qu'un algorithme génétique soit efficace, il FAUT une fonction d'évaluation qui augmente "progressivement" à mesure qu'on s'approche de la bonne solution.
une fonction d'évaluation qui respecte le critère précédent est par exemple celle consistant à mesurer de quelle distance le robot s'est rapproché de la sortie par rapport à sa position de départ ("MaximizeExitProximity") ; le problème est que l'évolution peut alors avoir tendance à se bloquer sur des étapes intermédiaires de parcours où il est nécessaire de s'éloigner (temporairement) de la sortie.
une troisième approche ("MaximizeCellsVisited") peut consister à compter le nombre d'emplacements visités, pour favoriser les robots explorant le labyrinthe par rapport à ceux qui "foncent dans le premier mur qu'ils rencontrent" et à ceux qui se bloquent dans un virage éloignant de la sortie ; mais ceci peut évidemment conduire à trouver des individus qui font une grande boucle dans le labyrinthe au lieu de trouver la sortie.
en fin de compte, la fonction d'évaluation la plus efficace pour résoudre ce problème est probablement une sorte de combinaison des trois précédentes (et peut-être d'autres !), telle que "MixedStrategy", qui vous permet de tester les combinaisons linéaires des trois précédentes.

Testez les fonctions d'évaluation présentées ci-dessus et comparez leurs efficacités respectives à faire émerger un individu trouvant la sortie du labyrinthe.

On pourra constater que si tout se passe bien, l'algorithme génétique est capable de trouver un chemin jusqu'à la sortie en environ 150 générations (voire moins) de taille égale à environ 200 individus (voire moins), ce qui implique qu'on a réellement testé au maximum 150x200~30000 hypothèses avant de trouver une solution convenable, alors que le cardinal total de l'espace exploré est 2⁹⁸~10³¹ (il y a 2 bits pour chacune des 49 cases, donc 98 bits) : ceci illustre la très grande capacité des algorithmes génétiques à "trouver une aiguille dans une botte de foin"...

Remarque : cette démonstration reste toutefois à but essentiellement illustratif et pédagogique, puisqu'il existe des algorithmes "classiques" capables de trouver la sortie de tout labyrinthe, et ce probablement de façon plus efficace que les algorithmes génétiques dans la présente démo...

Exercice 3 : apprentissage d'un comportement de robot

Pour commencer, visualisez l'environnement dans lequel évolue le "robot", et voyez le comportement inefficace du robot quand son "cerveau" neuronal est inadapté :

dans un "terminal", faire java -jar demo-GA-testAnimat.jar ratherStupidBrain.dat, puis appuyez sur le bouton start.

Le but serait que le robot explore l'espace pour y trouver et "manger" la "nourriture" (les F, comme Food, disséminés aléatoirement sur la grille), tout en ne consommant pas le "poison" (les P disposés eux-aussi aléatoirement) s'il vient à passer dessus.

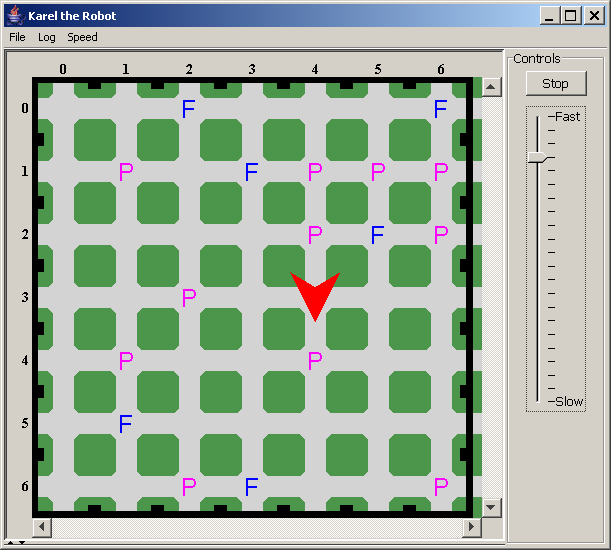
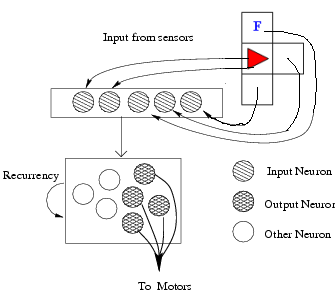
Le comportement du robot est déterminé par un petit réseau neuronal totalement bouclé(donc ayant un "état" interne) dont les sorties décident de son action (tourner, avancer, manger) en fonction de ce qu'il perçoit (présence de mur,de nourriture ou de "poison" juste en face, en face à gauche ou en face à droite). Ce réseau, illustré ci-dessus à droite, possède 5 entrées correspondant à 5 "senseurs" locaux (présence ou non de "quelque chose" là où il se trouve et sur les 3 cases adjacentes face/gauche/droite, "odeur" ou non de nourriture) et 10 neurones totalement connectés entre eux, dont 4 servent de sorties déterminant le comportement du robot : une sortie détermine s'il faut avancer, une autre s'il faut pivoter à droite, une troisième s'il faut pivoter à gauche, et la dernière sortie décide si le robot tente de "manger" ce qui serait éventuellement présent là où il se trouve. Le réseau contient donc 160 poids de connexions et biais pour lesquels il s'agit de trouver une combinaison de valeurs telle que le comportement résultant du robot soit le plus proche possible de celui recherché (ie trouver et manger tous les F, mais ne manger aucun P).

Il s'agit donc d'un problème d'apprentissage non-supervisé, au sens où on n'indiquera pas au réseau quelle décision prendre (donc quelles sorties produire) en fonction de ses entrées, et où ce qu'on cherche à optimiser n'est donc pas une simple erreur entre sorties désirées et sorties obtenues, mais un critère autre, en l'occurence la proportion de F "mangés" (diminuée du nombre de P consommés). On va effectuer cet apprentissage non-supervisé en utilisant des algorithmes génétiques, avec comme fonction d'évaluation ("fitness") la mesure (nbFood-nbPoison)/maxFood, où nbFood et nbPoison sont les quantités respectives de F et P "mangés" et maxFood la quantité totale de F disponibles ; pour que le comportement appris soit "général", cette mesure de fitness est moyennée sur N (=5) simulations du même robot dans des environnements aléatoires différents (seules les positions des F et des P variant), avec à chaque fois une position initiale et orientation initiale aléatoires pour le robot. Le codage employé pour le génome est ici directement la représentation binaire des 160 valeurs des poids et biais (autrement dit, une mutation appliquée correspond à inverser 1 bit de l'encodage IEEE-754 d'un de ces double).

Pour démarrer l'apprentissage par algorithmes génétiques, exécutez le fichier demo-GA-animat.jar (double-cliquez dessus, ou bien faire java -jar demo-GA-animat.jar dans un "terminal").

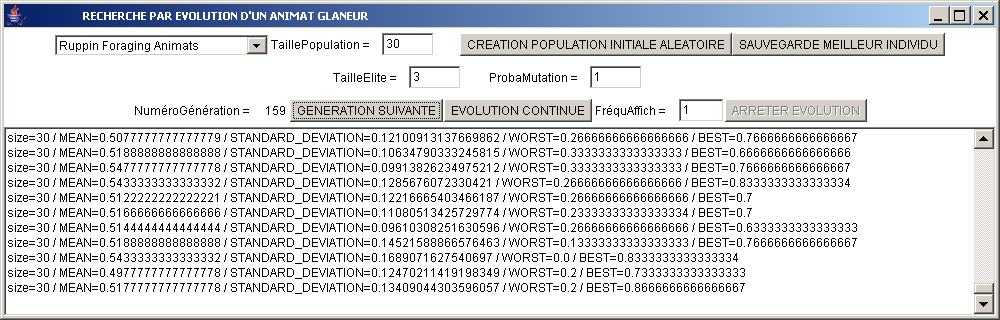
Créez une population initiale.
Faire évoluer la population : à chaque génération (ou bien toutes les G générations, si une valeur G est mise dans frequAffich) sont affichées diverses évaluation de la population : moyenne, ecart-type, minimum et enfin et surtou maximum de la fitness. A votre avis, pourquoi l'évaluation du meilleur individu (dernière valeur de chaque ligne) n'est-elle pas strictement croissante, même quand tailleElite>0 ?
Poursuivre l'évolution jusqu'à obtenir une génération dont le meilleur individu ait un score > 0.8 (voire même, idéalement, >0.9)
Arrêtez alors l'évolution, et sauvegardez le meilleur individu.
Testez le comportement de cet indivividu en lançant, dans un terminal la commande suivante :
java -jar demo-GA-testAnimat.jar evolved-xxgen-blaBla.dat
où evolved-xxgen-blaBla.dat doit être remplacé par le nom exact du fichier qui a été créé par la sauvegarde du meilleur individu.
Compte tenu des exercices précédents de ce TP, et aussi de ce qui a été évoqué (durant les séances consacrées au réseaux neuronaux) sur l'influence des valeurs absolues des poids d'un réseau sur sa "complexité", quelles modifications pourrait-on envisager dans la façon d'utiliser les Algorithmes Génétiques sur ce problème, en vue d'obtenir des résultats encore plus satisfaisants ?